数组

数组是长度受限的线性表
数组的定义：存储相同数据类型的一块连续的存储空间。

数组的存储

顺序存储

无论是高维数组还是一维数组，最终落实到具体的存储上都是一维的形式，只是地址搜索格式不太一样。

一维数组寻址公式

$Loc(i)=Loc(0)+i*s$

$0≤i≤n-1$

其中，p为首地址，s为每个元素占的空间
二维数组寻址公式
高维数组的寻址就会涉及到是按照什么顺序排列的，设二维数组A[m][n],数组有m行，n列。如果是按照行排列，寻址公式为：

$Loc(i,j)=Loc(0,0)+(i*n+j)*s$

$0≤i≤m-1, 0≤j≤n-1$

其中，s为每个元素占的空间。如果是按照列排序则i,j互换即可。
高维数组寻址公式
高维数组寻址就是类比二维数组。

稀疏矩阵

矩阵不一定都是放满数据的，对于那种没有放满的矩阵可以进行压缩。

对称矩阵
只要用一个n*(n+1)/2的一维数组存放即可。搜索具体值的公式是：
$a[i][j]=A[k]$
其中， $k=\begin{gathered} i*(i-1)/2+j-1 & i≥j\\ j*(j-1)/2+i-1 & i<j \end{gathered}$
三对角阵
主对角线和其两侧的位置有元素
$b[i][j]=B[k]$

$k=2*i+j-3$
稀疏矩阵
只有零星位置存在元素，其他均为0，对于这种矩阵，采用三元组方式进行存储，其中三元组又分为顺序存储和链式存储两个方法。三元组<row,col,item>
三元组顺序存储
！！！三元组的顺序存储一定要有一个标头一样的东西记录矩阵是几行几列的，有几个非零元素
三元的顺序存储方式如图

上述内容是按照行优先进行排列。蓝线部分就是标头，存放稀疏矩阵的一些信息。
对于矩阵有转置操作，下面介绍如何实现稀疏矩阵的三元组顺序存储的转置。、
对于矩阵的转置本质就是将行变成列，列变成行，其实只要将三元顺序存储的行和列互换就行，但是互换后顺序是错误的，所以转置的本质就是对三元组信息进行重新排序，此处介绍两个排序算法。
- 算法一（简单转置）
  扫描整个三元组表，按列的顺序从1-n一次扫描整个三元组，找到正确的排序。
  这种方法可以保证原来的行序是应为转置前的三元组表格就是按照由小到大排列的。
  这种方式的缺点是效率低下，每次都要遍历整个三元组，其复杂度为O(矩阵行数*矩阵非零元素个数)
- 算法二（快速转置）
  按照原先三元组的表格，找到每一个三元组转置后的位置再放入。这种方法的时间复杂度小，但是如何确定转置后的位置是一个问题。所以此处引入两个重要的数组：转置后每行元素个数num[n],转置后每行第一个非零元素在新三元组表的位置pos[n]。利用这两个数组可以实现放入位置的定位。其复杂度为O(矩阵非零元素个数)具体操作如下：
  1. 遍历三元组表格得到转置后每行的元素个数，放入num[n]中。
  2. 利用这个num[n]数组求出每行第一个非零元素在新三元组表中位置，放入pos[n]数组中，此步骤不用遍历数组。
  3. 遍历整个三元组表格，根据原先表格的列号和pos[n]数组，按次序照着位置放入数据。没用到一次pos[n],pos[n]++。
三元组链式存储（十字链表）
十字链表存放稀疏矩阵其实与原来的矩阵样式很像，其本质是多个带表头的单链表。这里要对一般链表结点进行一些修改，添加down和right两个指针。如图示：

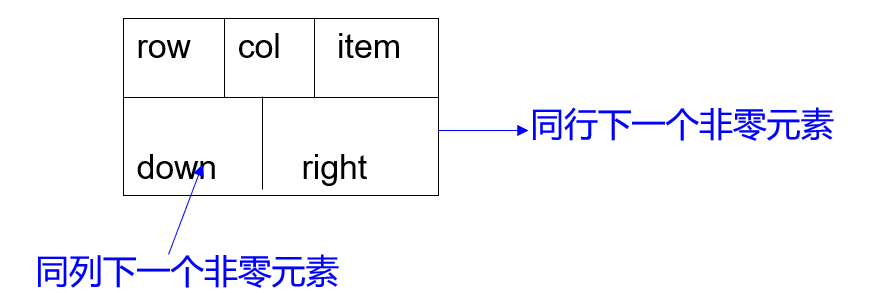
最后呈现出的状态如图：

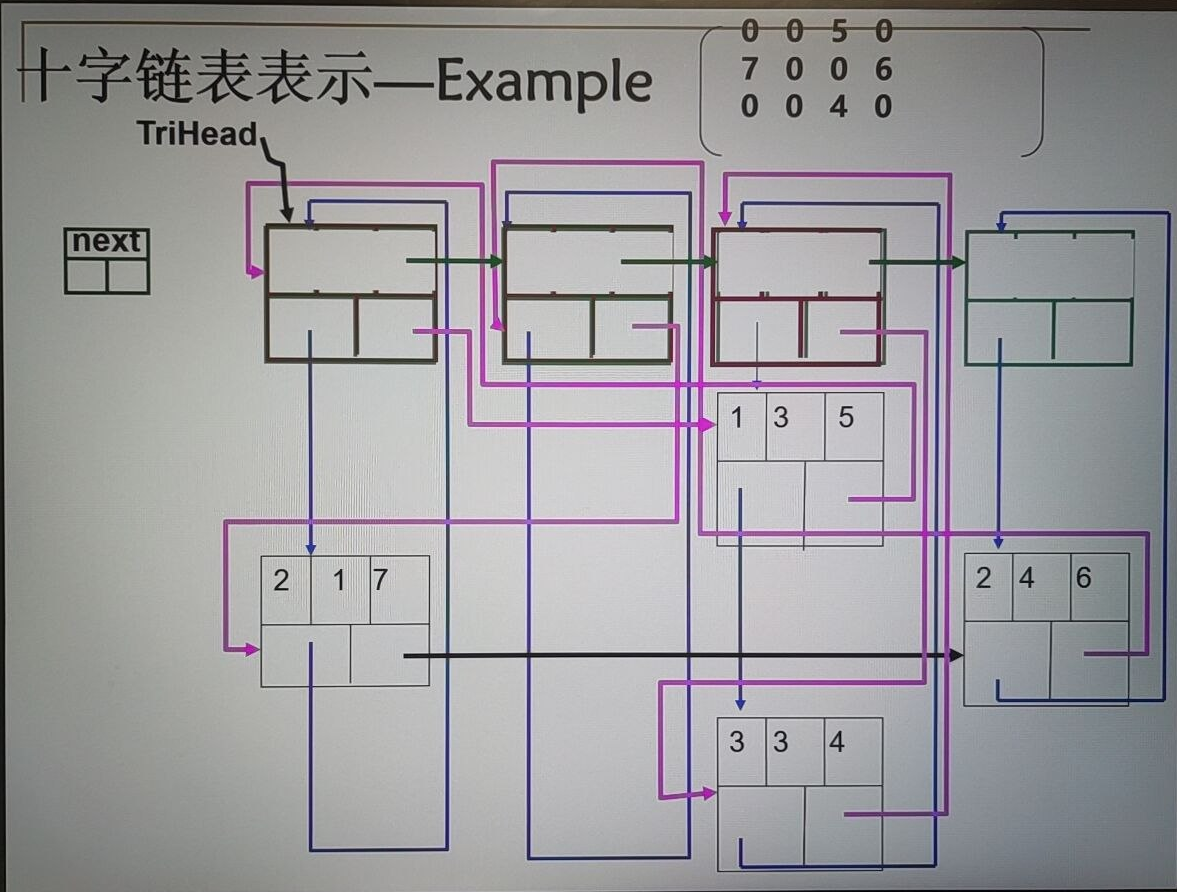
注意点：
- 头结点设计：next,down,right三个指针