图

图是一种一对多，多对多的非线性结构，在离散数学中是非常重要的内容，他的应用非常广泛，他的最重要的功能是寻找最短路径。数据结构中的图除了会介绍离散数学中基本的内容，更加注重图的存储结构，基本操作和一些关于图的重要算法。

基本概念

1. 定义：G=（V,E），其中V是数据元素的集合（可以理解为顶点集合），E是数据元素的关系集合（可以理解为边集合。<v,w>表示从v到w的一条路径。
2. 无向图与有向图：顶点对是否是有序的，有序为有向图<v,w>，无序为无向图(v,w)。数据结构这里要设置一些限制，数据结构的图不含环(<v,v>)和多重边的情况
3. 图的一些术语
   • 完全图：n个顶点，n(n+1)/2条边
   • 权
   • 邻接点：一条弧两端的点
   • 子图
   • 顶点的度
   • 路径
   • 简单路径和回路：经过顶点不重复的路径是简单路径；路径开始和结束是同一个顶点则为回路
   • 连通图和连通分量（无向图，极大连通子图）
   • 强连通图和强连通分量（有向图）
   • 生成树：极小连通子图
4. 基本操作
   • 插入顶点
   • 插入边
   • 删除顶点和附属边
   • 删除边
   • 取边上权
   • 取邻接点
   • 取下一个邻接点
   • 遍历图
   • 图判空

图的存储结构

作为一个复杂的结构，图的存储结构有4种，分别是邻接矩阵、邻接表、邻接多重表、十字链表。一般来说，图的存储按照具体需求来选择。

邻接矩阵（不易插入删除）

1. 邻接矩阵其实和离散数学中的关系矩阵一样，就是建立一个顶点的方阵，在无向图中如果顶点与顶点之间有关系（有边），则对应的元素值为1，其他为0。在有向图中顶点与顶点之间有关系，则对应元素是弧上权值，如果无法直接到达则元素为∞。

   $$arcs[i][j]=\begin{gathered} 1 & 如果<i,j>∈E或者(i,j)∈E\\ 0 & 否则 \end{gathered}$$

2. 结构
   邻接矩阵的存储示意图
   

3. 类模板设计及操作实现

    template <class ElemType>
   class AdjMatrixUndirGraph
   {
   protected:
    int vexNum, vexMaxNum, arcNum;
    int **arcs;
    ElemType *vertexes;
    mutable Status *tag;
   public:
     AdjMatrixUndirGraph(ElemType es[], int vertexNum,
               int vertexMaxNum=DEFAULT_SIZE);
     AdjMatrixUndirGraph(int vertexMaxNum=DEFAULT_SIZE);
     ~AdjMatrixUndirGraph();
     void Clear();
     bool IsEmpty();
     int GetOrder(ElemType &d) const;
     Status GetElem(int v, ElemType &d) const;
     Status SetElem(int v, const ElemType &d);
     int GetVexNum() const;
     int GetArcNum() const;
     int FirstAdjVex(int v) const;
     int NextAdjVex(int v1, int v2) const;
     void InsertVex(const ElemType &d);
     void InsertArc(int v1, int v2);
     void DeleteVex(const ElemType &d);
     void DeleteArc(int v1, int v2);
     Status GetTag(int v) const;
     void SetTag(int v, Status val) const;
     AdjMatrixUndirGraph(const
                AdjMatrixUndirGraph<ElemType> &g);
     AdjMatrixUndirGraph<ElemType> &operator =(
               const AdjMatrixUndirGraph<ElemType> &g);
     void Display();
   };

   求第一个邻接点序号

   template <class ElemType>
   int AdjMatrixUndirGraph<ElemType>::FirstAdjVex(int v) const
   {
      if (v < 0 || v >= vexNum)
            throw Error("v不合法!");
      for (int u=0; u < vexNum; u++)
      if (arcs[v][u] != 0)
                     return u;
         return -1;
   }

   求下一个邻接点序号

   template <class ElemType>
   int AdjMatrixUndirGraph<ElemType>::NextAdjVex(int v1,
         int v2) const
   {
      if (v1 < 0 || v1 >= vexNum)   throw Error("v1不合法!");
      if (v2 < 0 || v2 >= vexNum)    throw Error("v2不合法!");
      if (v1 == v2) throw   Error("v1不能等于v2!");
      for (int u=v2 + 1; u < vexNum; u++)
      if (arcs[v1][u] != 0)
                  return u;
         return -1;
   }

   插入顶点

   template <class ElemType>
   void AdjMatrixUndirGraph<ElemType>::InsertVex(const ElemType &d)  {
         if (vexNum == vexMaxNum)
            throw Error("图的顶点数不能超过允许的最大数!");
         vertexes[vexNum]=d;
         tag[vexNum]=UNVISITED;
         for (int v=0; v <= vexNum; v++) {
      arcs[vexNum][v]=0;
      arcs[v][vexNum]=0;
         }
         vexNum++;
   }

   插入边

   template <class ElemType>
   void AdjMatrixUndirGraph<ElemType>::InsertArc(int v1,
         int v2)  {
      if (v1 < 0 || v1 >= vexNum)    throw Error("v1不合法!");
      if (v2 < 0 || v2 >= vexNum)    throw Error("v2不合法!");
      if (v1 == v2)    throw Error("v1不能等于v2!");
      if (arcs[v1][v2] == 0)	{
      arcNum++;
      arcs[v1][v2]=1;
            arcs[v2][v1]=1;
      }
   }

   删除顶点：删除顶点比较复杂，如果顶点是最有一个，则可以直接顶点数减一删除；如果是中间的顶点，则先删除依附于顶点的边，然后将最后的顶点的行列移到被删除点的位置上，最后顶带点数减一，实现删除。

   template <class ElemType>
   void AdjMatrixUndirGraph<ElemType>::DeleteVex(const ElemType &d)  {
      int v;
      for (v=0; v < vexNum; v++)
         if	 (vertexes[v] == d)     break;
      if (v == vexNum)  throw Error("图中不存在要删除的顶点!");
      for (int u=0; u < vexNum; u++)
         if (arcs[v][u] == 1) {
      arcNum--;
            arcs[v][u]=0;
            arcs[u][v]=0;
            }
      vexNum--;
      if (v < vexNum) {
            vertexes[v]=vertexes[vexNum];
            tag[v]=tag[vexNum];
            for (int u=0; u <= vexNum; u++)
         arcs[v][u]=arcs[vexNum][u];
            for (int u=0; u <= vexNum; u++)
               arcs[u][v]=arcs[u][vexNum];
      }
   }

   删除边

   template <class ElemType>
   void AdjMatrixUndirGraph<ElemType>::DeleteArc(int v1, int v2)
   {
      if (v1 < 0 || v1 >= vexNum)    throw Error("v1不合法!");
      if (v2 < 0 || v2 >= vexNum)    throw Error("v2不合法!");
      if (v1 == v2)    throw Error("v1不能等于v2!");
      if (arcs[v1][v2] != 0)	{
      arcNum--;
            arcs[v1][v2]=0;
            arcs[v2][v1]=0;
      }
   }

邻接表

邻接表是邻接矩阵的改进，主要解决的问题是边数较小的情况下的邻接矩阵比较浪费空间的问题。具体的改进措施是将每一行改为一个单链表。
具体的无向图结点和邻接表设计如下图：

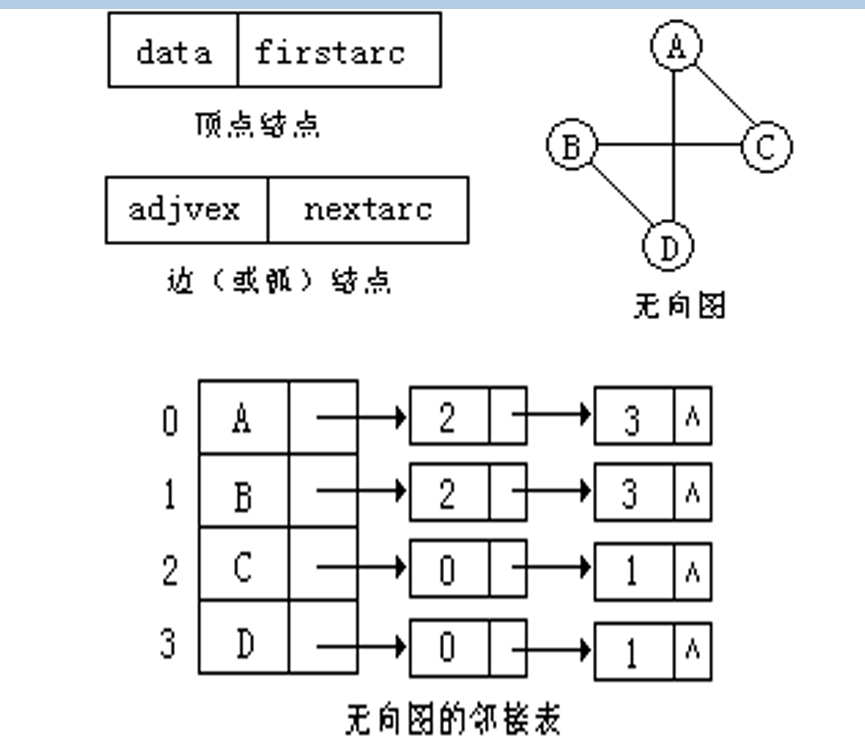
无向图的度计算是通过计算每个顶点的链表长度实现的，但是有向图的度比较难计算，而且还分为入度、出度，所以引入逆邻接表的概念。
逆邻接表：反应顶点的入度情况。
因此，对于有向图，领接表链表结点表达出度，逆邻接表链表结点表达入度
有向图领接表结构

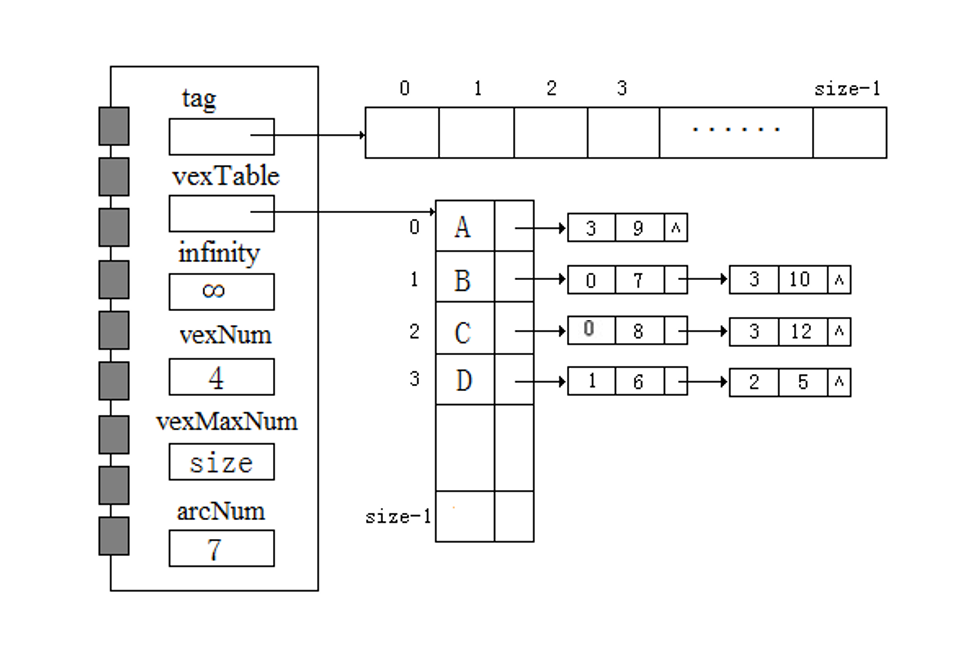
对于邻接表的模板设计这里不多做赘述，只讲述一下删除结点的方法。
邻接表删除：和邻接矩阵的删除方法一样。

邻接多重表

邻接多重表是邻接表的改进，主要解决的问题是无向图中，给边加标记时会出现需要修改两次的情况。
这里要修改结点设置，边结点有六个域,分别是tag标记域，标记该边是否被处理，weight为信息域，存储边权值，adjvex1与adjvex2为顶点域，nexttarc1为链接指针域，指向下一个与第一个顶点链接的点，nexttarc2指向下一条依附于第二个顶点的边。顶点结点含两个域，一个是data数据域，另一个是firstarc链接指针。具体设置如图

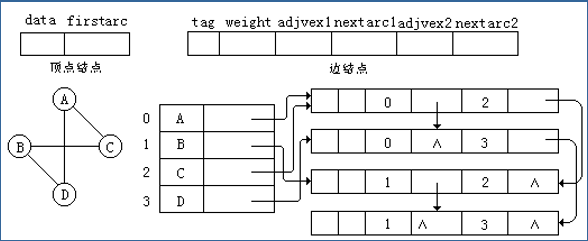
十字链表

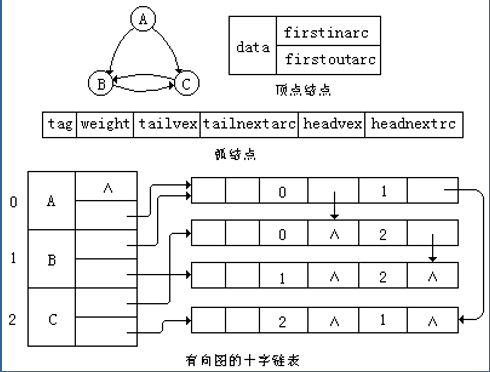
邻接多重表是对于无向图的邻接表改进，对于有向图也要有改进，有向图的链式结构是十字链表。有向图有入度与出度的概念，所以有时操作需要涉及到邻接表和逆邻接表，这里的十字链表就是将两个表融合到一起。十字链表的边结点也有六个域，tag为标记域，weight为弧的信息域，tailvex和headvec表示弧头和弧尾结点，tailnextarc指向的是下一个以tailvex为始点（弧尾）的弧，headnetarc指向下一个以headvec为终点（弧头）的弧。弧尾的意思是始点，弧头的意思是终点。顶点结点有两个域，一个是firstinarc指向第一个以该结点为终点的弧，firstoutarc指向第一个以该顶点为始点的弧。

图的遍历与连通性

图的遍历是非常重要的图的操作。访问所有的顶点，且每个顶点只访问一次，我们需要设置一个辅助数组tag[]来确定是否已经访问过该结点。对于图的遍历，主要有两个方法，深度优先遍历和广度优先遍历。

深度优先遍历

1. 深度优先遍历基于深度优先搜索（DFS），先从一个顶点出发，访问该顶点后依次从该顶点访问任一没有被访问的邻接顶点，直至所有与该顶点路径相通的顶点都被访问过为止。 利用递归解决。
   在整个DFS的过程中，首先要选一个起始顶点，这个顶点可以是任意的。
   
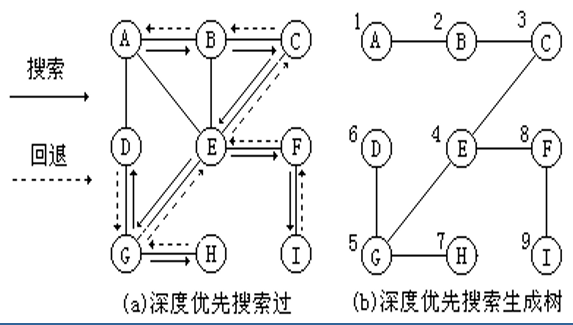
   ==这里要强调一点，深度优先搜索是搜索一个点的，而深度优先遍历是遍历所有的点，是反复调用DFS。==

2. 深度优先遍历可以有递归与非递归的方法实现。递归是反复调用深度优先搜索，非递归是利用栈来实现的，具体实现操作是顶点入栈，出栈标记访问，然后看是否存在未被访问的邻接点，存在，则邻接点入栈。

   深度优先搜索(递归)

   template <class ElemType>
   void DFS(const AdjMatrixUndirGraph<ElemType> &g,
         int v,   void (*Visit)(const ElemType &))   {
      ElemType e;
      g.SetTag(v, VISITED);
      g.GetElem(v, e);
      Visit(e);
      for (int w=g.FirstAdjVex(v); w != -1;
                  w=g.NextAdjVex(v, w))
            if (g.GetTag(w) == UNVISITED)
         DFS(g, w, Visit);
   }

   深度优先遍历（递归）

   template <class ElemType>
   void DFSTraverse(const AdjMatrixUndirGraph<ElemType> &g,
      void (*Visit)(const ElemType &))  {
      int v;
      for (v=0; v < g.GetVexNum(); v++)
         g.SetTag(v, UNVISITED);
      for (v=0; v < g.GetVexNum(); v++)
         if (g.GetTag(v) == UNVISITED)
            DFS(g, v, Visit);
   }

3. 深度优先遍历的算法复杂度
   如果是邻接表：n个顶点，2e个边界点，复杂度为 $O(n+e)$
   如果是邻接矩阵：搜素一个顶点的所有关联边要 $O(n)$，整体的遍历要 $O(n^2)$

广度优先遍历

1. 广度优先遍历基于广度优先搜索。从一个顶点出发，访问该顶点的各个未被访问过的邻接顶点w1,w2,…wk,然后再访问w1,w2,…wk所有未被访问过的邻接顶点，直至所有结点都被访问
   
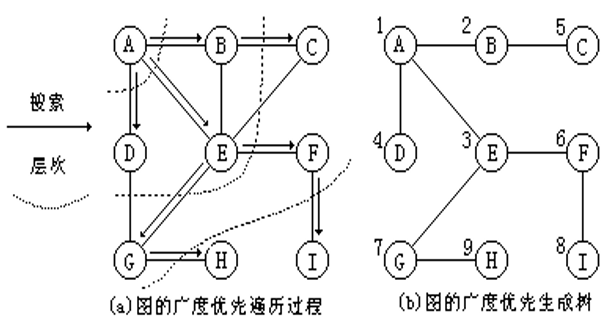
2. 对广度优先遍历的方法也是采用队列实现，
   广度优先搜索

   template <class ElemType>void BFS(const AdjMatrixUndirGraph<ElemType> &g,
      int v, void (*Visit)(const ElemType &)){
      LinkQueue<int> q;
      int u, w;
      ElemType e;    g.SetTag(v, VISITED);   g.GetElem(v, e);
      Visit(e);	 q.EnQueue(v);
      while (!q.IsEmpty())  {	q.DelQueue(u);
         for (w=g.FirstAdjVex(u); w != -1; w=g.NextAdjVex(u, w))
            if (g.GetTag(w) == UNVISITED){
               g.SetTag(w, VISITED);  g.GetElem(w, e);
         Visit(e);   q.EnQueue(w);
               }
      }
   }

   广度优先遍历

   template <class ElemType>
   void BFSTraverse(const AdjMatrixUndirGraph<ElemType> &g,
      void (*Visit)(const ElemType &)) {
      int v;
      for (v=0; v < g.GetVexNum(); v++)
         g.SetTag(v, UNVISITED);
      for (v=0; v < g.GetVexNum(); v++)
         if (g.GetTag(v) == UNVISITED)
            BFS(g, v, Visit);
   }

3. 广度优先遍历的算法复杂度和深度优先遍历的算法复杂度一致。

连通分量

对于非连通图，需要调用n次深度或广度优先遍历实现遍历，由遍历所得的树就叫做生成树，而非连通图的所有生成树组成了非连通图的生成森林。

最小生成树

对于一个网络可以有很多的生成树来连接，但是实际应用上，我们要考虑最优的网络保证最低的成本，所以这里就需要最小生成树。
重要性质：如果一条边是连通图里的权值最小的边，那么这条边一定在最小生成树里
最小生成树有两个计算的算法，分别是克鲁斯卡尔算法和普利姆算法。

克鲁斯卡尔算法

1. 克鲁斯卡尔算法就是将所有的边从小到大排列，然后不停地将边添加到生成树集合之中。所以它也被称为“加边法”，这里需要注意的是加边的条件是边的两个顶点是属于不同的集合。

   • 初始化，在并查集中，连通图的每一顶点独立成一个等价类，连通图的所有边建立最小堆，最小生成树T中没有任何边，T中边数计数器i为0；
   • 如果T中边的条数i比顶点数少1，则算法结束；否则继续步骤（3）；
   • 选取堆顶元素代表的边（v，u），同时调整堆；
   • 利用并查集的运算检查依附于边（v，u）的两个顶点v和u是否在同一个连通分量(并查集的同一子集)上，如果是则转步骤（2）；否则继续步骤（5）；
   • 将边（v, u）加入到最小生成树T中，i++，同时将这两个顶点所在的连通分量合并成一个连通分量(即并查集中的相应两个子集合并成一个子集)，继续步骤（2）。
     注意要点：生成树集合的边数是n-1就可以停止进行运算；克鲁斯卡尔算法用并查集和最小堆实现
     具体例子:
     

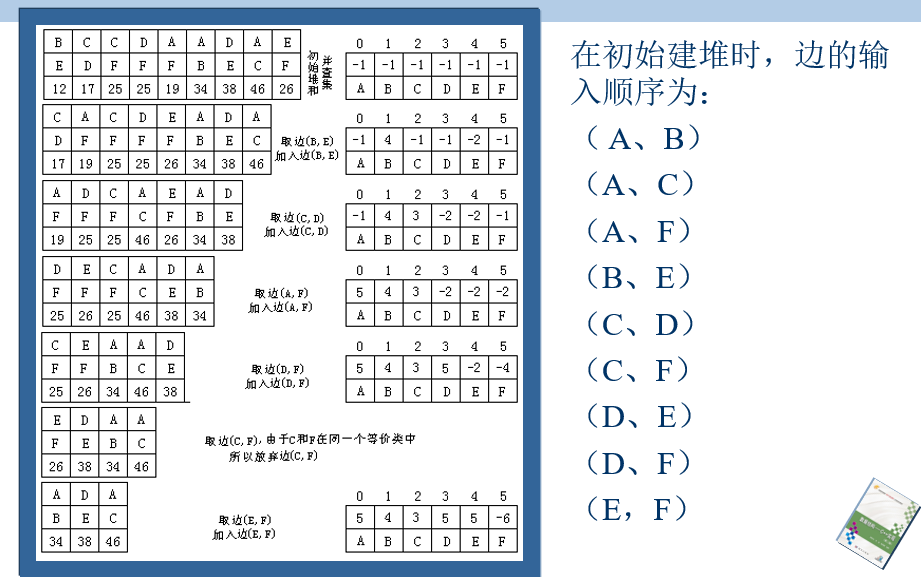
2. 代码实现：

template <class ElemType, class WeightType>
void MiniSpanTreeKruskal
    (const AdjMatrixUndirNetwork<ElemType, WeightType> &g){
    int count, VexNum=g.GetVexNum();
    KruskalEdge<ElemType, WeightType> KEdge;
    MinHeap<KruskalEdge<ElemType, WeightType> >
    ha(g.GetEdgeNum());
    ElemType  *kVex, v1, v2;
    kVex=new ElemType[VexNum];
    for (int i=0; i < VexNum; i++)
          g.GetElem(i, kVex[i]);
    UFSets<ElemType> f(kVex, VexNum);
   for (int v=0; v < g.GetVexNum(); v++) //将所有边插入堆
         for (int u=g.FirstAdjVex(v); u >= 0; u=g.NextAdjVex(v, u))
      if (v < u)	{ g.GetElem(v, v1); g.GetElem(u, v2);
         KEdge.vertex1=v1;  KEdge.vertex2=v2;
                  KEdge.weight=g.GetWeight(v, u);  ha.Insert(KEdge);
      }
      count=0;
      while (count < VexNum - 1)  { ha.DeleteTop(KEdge);
                  v1=KEdge.vertex1;  v2=KEdge.vertex2;
            if (f.Differ(v1, v2))  {cout << "边:( " << v1 << ", " << v2
                        << " ) 权:"<< KEdge.weight << endl ;
               f.Union(v1, v2); count++;
            }
            }
   }

3. 克鲁斯卡尔算法时间复杂度
   克鲁斯卡尔算法的时间复杂度从两个方面分析，一是建立最小堆的复杂度，对于n个结点，e条边的网络，最小堆的时间复杂度是$O(elog_2e)$;二是最小生成树的复杂度，这个过程中最多调用e次堆的删除操作、2e次并查集的查找操作和n-1次并查集的合并操作，他们分别的复杂度为$O(elog_2e)$，$O(elog_2e)$和$O(n)$,所以综合复杂度为$O(elog_2e)$，因此，也可看出克鲁斯卡尔算法适合稀疏连通网络的最小生成树

普里姆算法

普里姆算法和克鲁斯卡尔算法其实是类似的，但是他不是找顶点分属不同集合的最小边，而是找已经在生成树内的点衍生出的最小边（这个边的另一个顶点不能在生成树集合内）。
这里需要一个辅助数组，来帮助计算，其中lowweight中存放顶点v到U中的各顶点的边上的当前最小权值(lowweight=0表示vU)；nearvertex记录顶点v到U中具有最小权值的那条边的另一个邻接顶点u（nearvertex=-1表示该顶点v为开始顶点）。 其形式如下图：

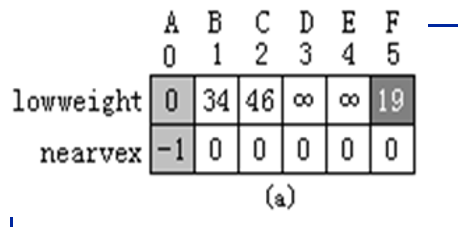
代码实现：

template <class ElemType, class WeightType>
void MiniSpanTreePrim(const AdjMatrixUndirNetwork<ElemType,
 WeightType> &g, int u0) {
     WeightType min;
     ElemType v1, v2;
     int vexnum=g.GetVexNum();
     CloseArcType<ElemType, WeightType> * closearc;
     if (u0 < 0 || u0 >= vexnum)   throw Error("顶点u0不存在!");
     int u, v, k;
     closearc=new CloseArcType<ElemType, WeightType>[vexnum];
     for (v=0; v < vexnum; v++)	{
	closearc[v].nearvertex=u0;
	closearc[v].lowweight=g.GetWeight(u0, v);
     }
     closearc[u0].nearvertex=-1;
     closearc[u0].lowweight=0;
     for (k=1; k < vexnum; k++) {
         min=g.GetInfinity();  v=u0;
         for (u=0; u < vexnum; u++)
           if (closearc[u].lowweight!=0
                         &&closearc[u].lowweight<min){
	       v=u;
                  min=closearc[u].lowweight;
	    }
       if (v != u0) {
           g.GetElem(closearc[v].nearvertex, v1); g.GetElem(v, v2);
	cout << "边:( " << v1 << ", " <<  v2 << " ) 权:"<< min << endl;
	closearc[v].lowweight=0;
	for (u=g.FirstAdjVex(v); u != -1 ; u=g.NextAdjVex(v, u))
 	  if (closearc[u].lowweight != 0 &&
		(g.GetWeight(v, u) < closearc[u].lowweight))	{
	     closearc[u].lowweight=g.GetWeight(v, u);
	     closearc[u].nearvertex=v;
	  }
       }
   }
  delete []closearc;
}

最短路径问题

从一个顶点到另一顶点可以有很多的路径，但是实际工程应用上我们希望路径越短越好。因为图存在这带权值与不带权值两种情况。对于不带权值