广义表

基本概念

  1. 定义：由n≥0个表元素α1 ,α2 , … , αn 组成的有限序列，其中表元素αi (1≤i≤n) 或者是一个数据元素 (可称为单元素或原子)，或者是一个表(称为子表)。记作
    LS = (α1 ,α2 , … , αn )
  2. 广义表的数据元素可以是单独一个元素也可以是一个表，所以其为多层次结构。
  3. α1为表头，其余的为表尾。
  4. 广义表中括号的重数为广义表的深度。
  5. 广义表的定义是递归的，所以广义表的深度可以是无穷。
  6. 广义表的操作有取表头，取表尾。
  7. 广义表最高一层的结点个数即为表长。
  8. 广义表中每个表都是带表头的，表头主要放引用次数信息。

广义表的存储

广义表采用链式存储方式，他的结点设计有一定的特殊性（采用联合体设计方式），包含三类数据，分别为1）表头的引用计数 2）单元素的元素值 3）表的指针
结点设计如图

广义表例子如图

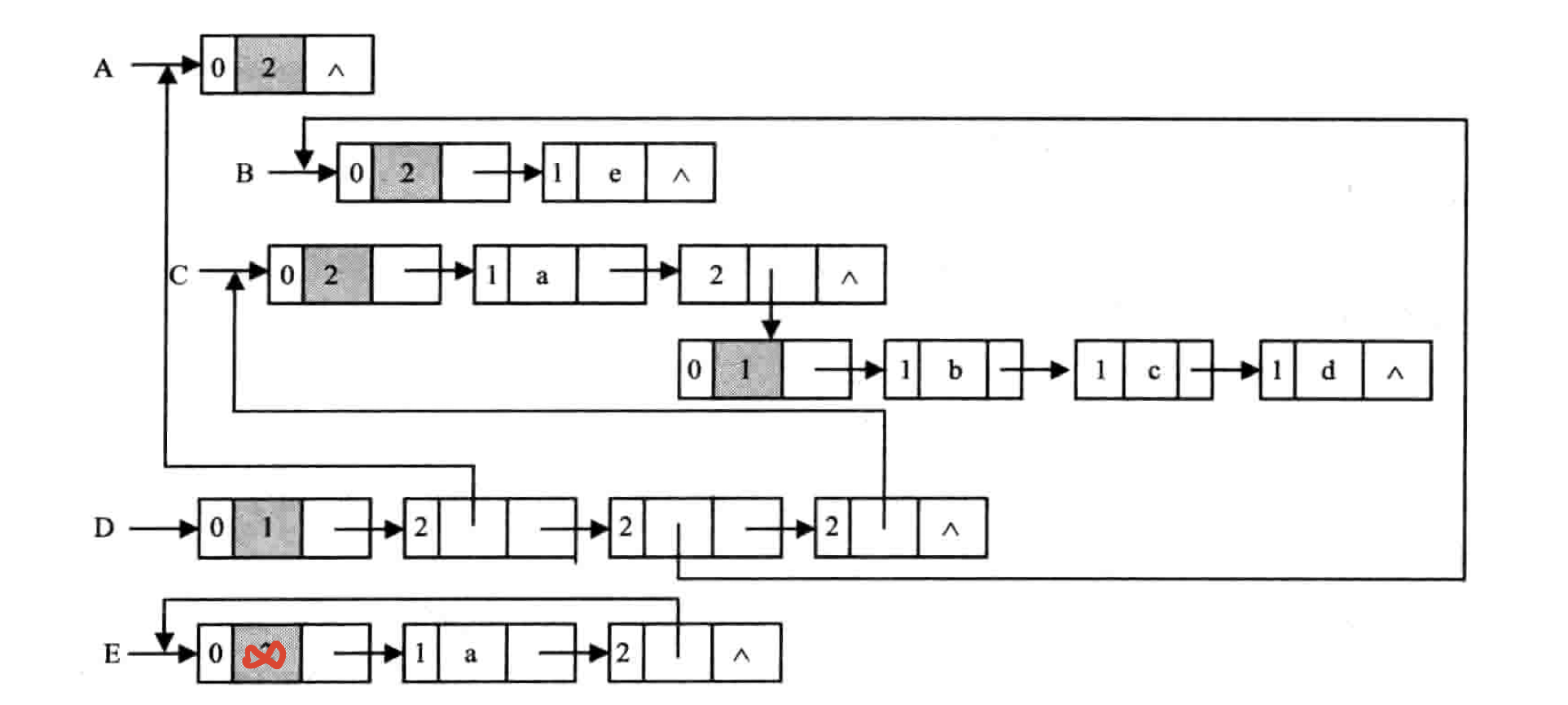
problem:表的深度怎么求？
利用递归求所有的字表层数加一。

广义表的结点和类定义

类定义

  class genlist 		//广义表类定义
{
  protected:
    glnode * first;                     //建立广义表的表头指针
    //自身属性相关的函数
    int depth (glnode * gl ) ;
    //计算非递归表( *gl )的深度
    glnode * copy (glnode * gl );
    //复制无共享且非递归表( *gl )
    int equal (glnode * s , glnode * t );
    //比较两个表( * s, * t ) 是否相等
    void Delete (glnode * gl ) ;            //释放广义表( * gl )
  public:
    genlist ( ) ;                //构造函数
  ~genlist ( ) ;               //析构函数
  int depth ( ) ;              //计算一个非递归表的深度
  void copy (const genlist & ls) ;   //广义表的复制
  glnode& head( );            //返回广义表第一个结点的tag及值
  genlist * tail( );           //返回表中第二个结点的指针
   glnode *First( );　　   　//返回广义表的第一个结点的指针
  glnode *next( glnode *elem);　
    //返回elem所指结点的直接后继结点的指针
}

注意点：在广义表的类定义中保护和公共部分都有求深度函数，公开的函数是对于保护函数的一个调用，而保护函数是一个递归函数。
具体实现：

  int genlist :: depth (glnode * gl )  //计算非递归广义表的深度
{
      if ( gl->tlink = = NULL ) return 1 ;      //空表的深度为1
      glnode * p = gl->tlink ;
      int m = 0 ;
    while (p->tlink != NULL)   {   //扫描广义表顶层的各个结点
        if (p ->tag= =2 )       {      //递归调用求子表结点的深度
      int n = depth (p->hlink) ;
            if  (m<n) m = n ;
        }
    p = p->tlink ;
  }
      return  m+1 ;
}

这里是不用计算单元素的表深度的，因为计算表头时已经包含了单元素。

广义表的应用（n元多项式的表达）

  1. n元多项式可以用广义表来实现，本质就是一个变元就是广义表的一层，只要将n元多项式按照不同的变元进行改写即可。此处仍然采用联合体方式设计广义表的结点
    具体设置如下图：

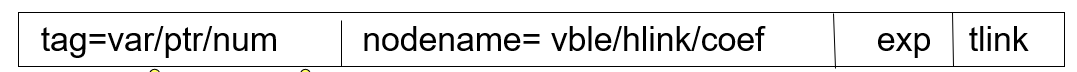
    其中，tag为var域，nodename存放变量，exp为0；tag为ptr域，nodename存放下一层变元指针，exp存放次数；tag为num，nodename存放系数，coef为系数值，exp为次数。

  2. 多项式结点定义如下

class polynode{
	polynode * tlink ;　　//同一层下一结点指针
	int exp ;　　　　　　//指数
	/*标志，是var时为表头结点，是ptr时为子表结点，是num时为原子结点*/
	triple tag ;
　　　	union  {　　　　　　　//联合
		char vble ;　　　　//表头结点中存放该链表基于的变元名
		polynode * hlink ;　//子表结点中存放指向系数子链表的指针
		int coef ;　　　　  //原子结点中存放实数型系数
	};
};
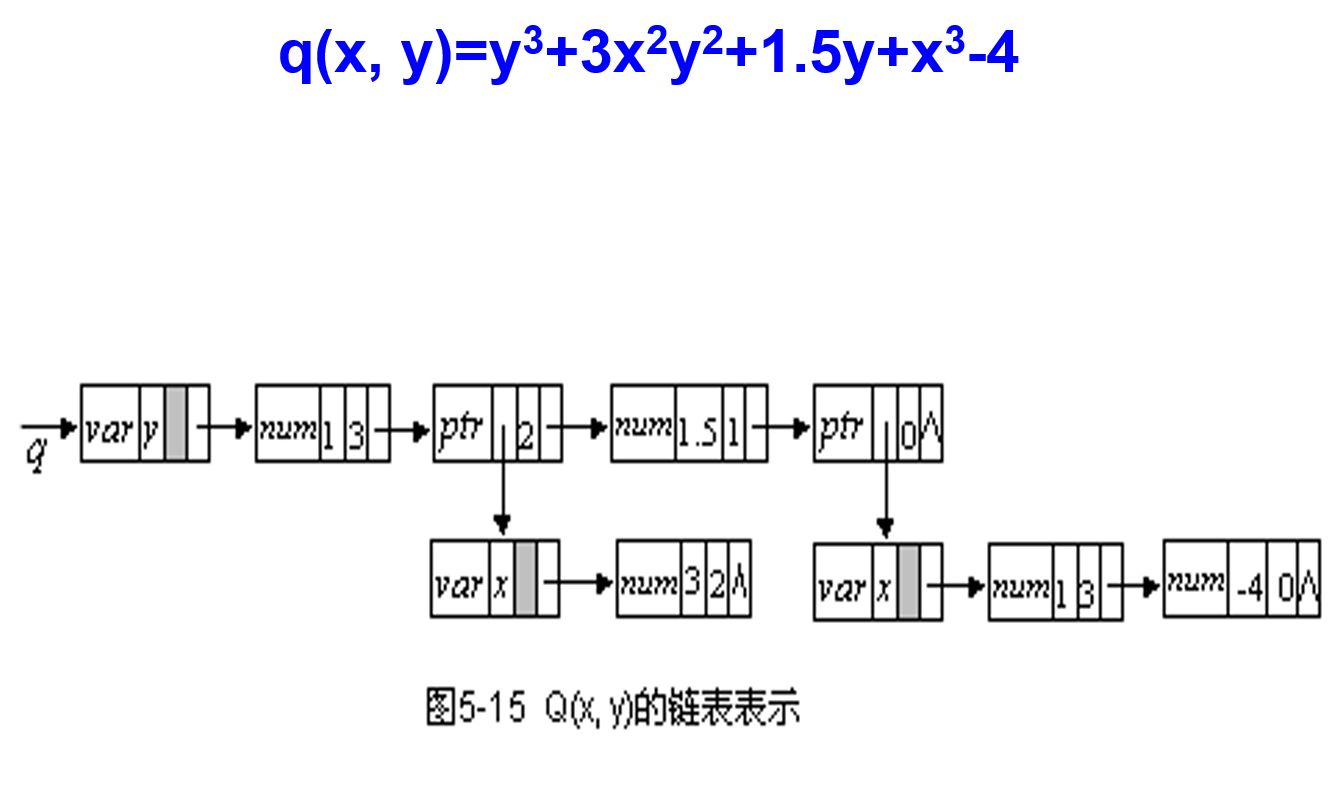
  1. n元多项式表达实例