二叉树

基本概念

树的基本概念

特点

当n = 0时，T称为空树；
如果n > 0，则树有且仅有一个特定的被称为根（root）的结点，树的根结点只有后继，没有前驱；
当n>1时，除根结点以外的其余结点可分为m(m>0)个互不相交的非空有限集T1、T2、…、Tm，其中每一个集合本身又是一棵非空树，并且称它们为根结点的子树（subtree）。

术语

结点（node）
结点的度（degree of node）
终端结点(terminal node)—叶子(leaf)
非终端结点(nonterminal node) —分支结点
树的度（degree of tree）
孩子(child)和双亲(parent)
兄弟(sibling)
堂兄弟
祖先(ancestor)
子孙（descendant）
结点的层次（level）
树的深度（depth）—高度（height）
有序树
无序树
森林(forest)

表示方式

嵌套集合
广义表
凹入表示

二叉树的基本概念

定义
二叉树BT是有限个结点的集合。当集合非空时，其中有一个结点称为二叉树的根结点，用BT表示，余下的结点（如果有的话）最多被组成两棵互不相交的、分别被称为BT的左子树（left subtree）和右子树（right subtree）的二叉树。

性质

最大度为2
二叉树的结点子树有左右之分
满二叉树是每层都是完整的二叉树
完全二叉树是只有最后几个结点没有的二叉树
有n(n>0)个结点的二叉树的分支数为n-1
顺序存储下，若i＝0，则 i 无双亲，若i＞0，则 i 的双亲为i/2-1
若2i+1<n，则 i 的左孩子为2i+1
若2i+2<n，则 i 的右孩子为2i+2
若i为偶数，且i≥1，则 i 是其双亲的右孩子，且其有编号为i-1左兄弟
若i为奇数，且i＜n-1，则 i 是其双亲的左孩子，且其有编号为i+1右兄弟

存储结构

二叉树的存储方式有两种，一个是顺序存储，另一个是链式存储

顺序存储

顺序存储便于查找数据，但是二叉树这种结构的数据在顺序存储情况下容易浪费空间资源，所以顺序存储一般只用在满二叉树或者完全二叉树。

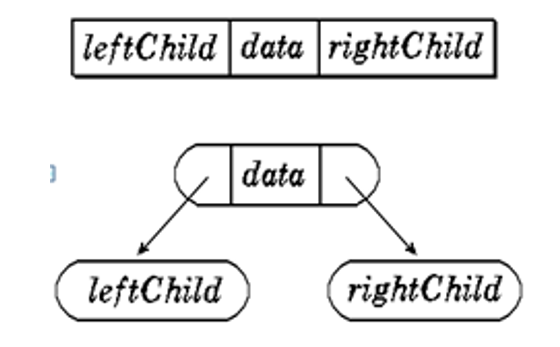
链式存储

一般的二叉树采用链式存储的方式存储。他有两个指针指向左右孩子。在有n个结点的链式存储

代码实现:

template <class ElemType>
struct BinTreeNode{
  ElemType data;				// 数据域
  BinTreeNode<ElemType>  *leftChild;	// 左孩子指针域
  BinTreeNode<ElemType>  *rightChild;	// 右孩子指针域
  BinTreeNode();		// 无参数的构造函数
  BinTreeNode(const ElemType &val
    BinTreeNode<ElemType> *lChild = NULL,
    BinTreeNode<ElemType> *rChild = NULL);
};

遍历方法

二叉树的遍历的方法有很多，包括前序遍历、中序遍历、后序遍历、层序遍历，对应的算法也有递归与非递归的实现。前中后的非递归算法都是由栈来实现，而层序遍历的非递归由队列实现。

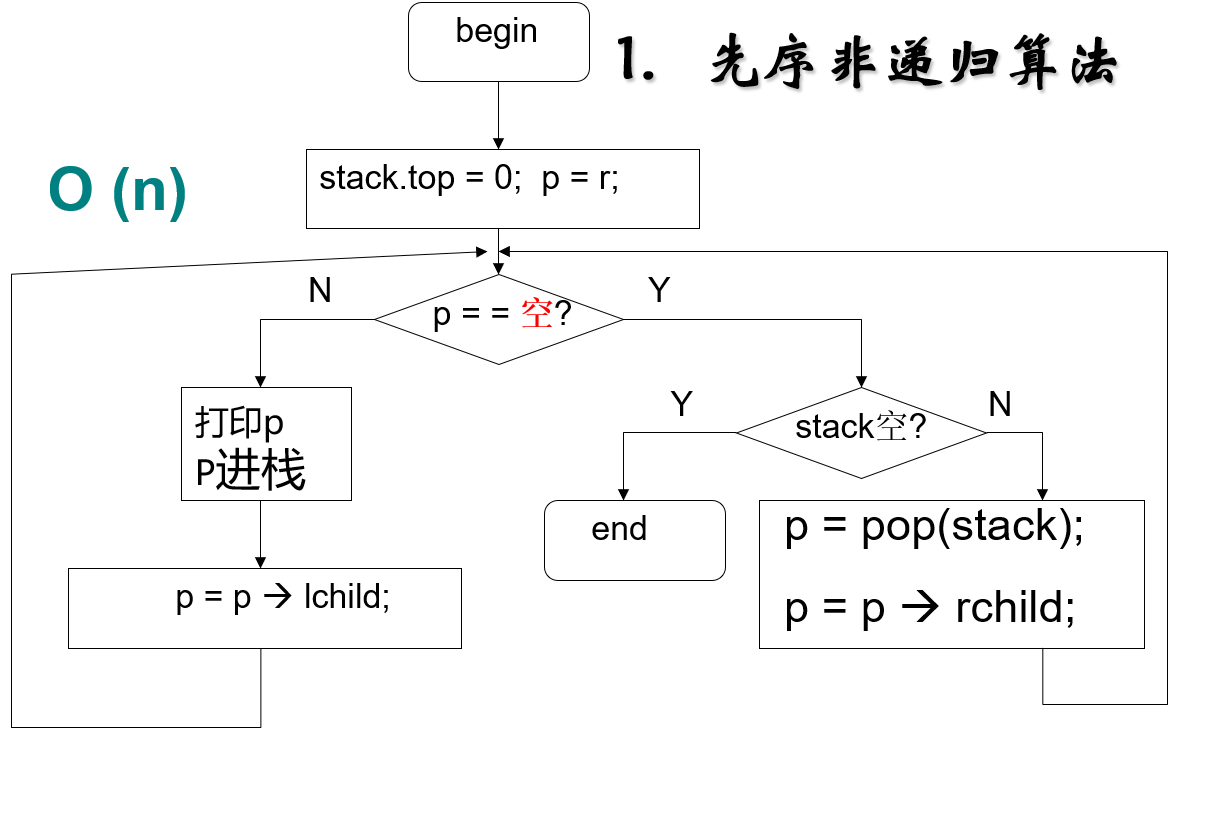
前序遍历

先访问根节点，然后是左节点，最后是右节点。
递归代码实现：

template <class Type> void BinaryTree<Type>::
PreOrder ( BinTreeNode <Type> *r )
{
  if ( r != NULL ) {
    cout << r→GetData( ) << endl;
    PreOrder ( r→GetLeftChild( ) );
    PreOrder ( r→GetRightChild( ) );
  }
}

对于前中后序遍历的递归算法实现都是如此，只要改一下具体的函数即可。
非递归实现（栈）
利用栈，来实现遍历
对于前序，在栈中先放根节点，然后放入其左节点，如果没有左右结点，就将该结点出栈，一直到栈为空停止。

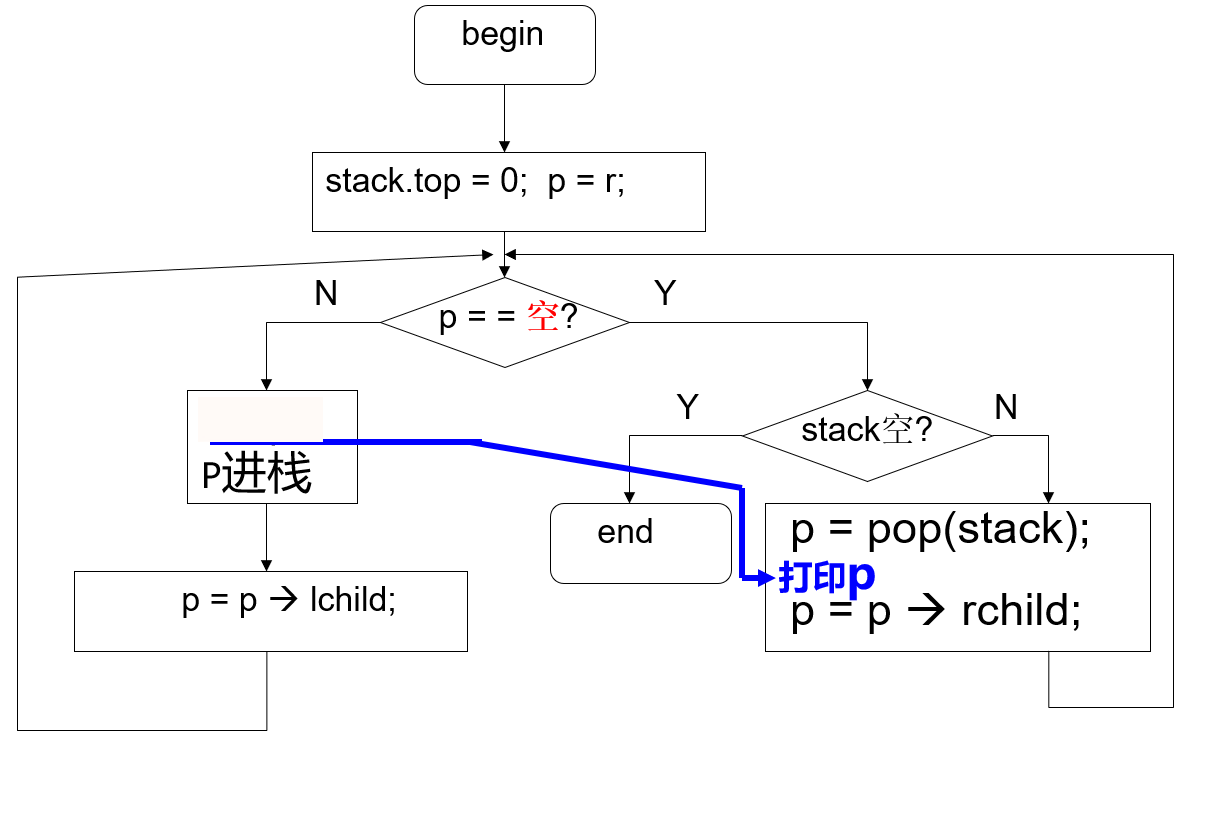
中序遍历

先访问左节点，然后是根节点，最后是右节点
非递归实现（栈）
利用栈来实现遍历
对于中序遍历，其实基本和前序遍历一致，就是打印的时间变化了，详细可以看流程图。

后序遍历

先访问左子树，然后是右子树，最后是根节点。
非递归实现（栈）
后序遍历仍然采用上述的方法进行遍历的会产生一个问题，一个叶子节点没有左右孩子，这是指针为空，应该是要出栈，但是如果该结点已经出栈了就没有了他的信息，无法获得所需要的其父亲结点的右孩子信息。所以这里有两个方法。一是利用两个一个栈用于存放结点的标记，二是使用一个栈，修改出栈逻辑。

利用两个栈
两个栈分别为结点栈和标记栈，其中标记栈标记的是对应节点的状态。0代表先不出站，1代表出栈。

P为空，此时应该出栈，出栈加判断：
tag栈顶元素为0，p = stack栈顶元素B，但stack不出栈，且tag栈顶元素修改为1，p = p->GetRightChild(); (继续遍历右子树)
P为空，此时应该出栈，出栈加判断：
tag栈顶元素为1，p = stack栈顶元素B，stack出栈，且tag出栈，此时真正“访问”p （即打印B）

利用一个栈
利用一个栈的方法就是要等到可以访问他的父亲结点时再将他出栈。

层序遍历

定义：所谓层次遍历(Levelorder Traversal)二叉树，是指从二叉树的第一层(根结点)开始，自上至下逐层遍历，在同一层中，则按从左到右的顺序对结点逐个访问。
层序遍历利用了队列来实现。具体实现的方法是：将根节点入队，如果有子节点就将子节点入队，在自己出队。每次看队头元素是否有子节点。
代码实现：

template <class Type> void BinaryTree<Type>::LevelOrder ()
{
  linkqueue <BinTreeNode * > q;
  BinTreeNode * p = root;
      if  (p )  q.EnQueue(p);
      While (!q.IsEmpty( )) {
                p = *q.DeQueue ();
                cout << p.GetData( ) << endl;
                if(p→GetLeftChild( ) ) q.EnQueue (p→GetLeftChild( ) );
                if(p→GetRightChild()) q.EnQueue(p→GetRightChild( ) );
  }
}

由遍历序列还原二叉树

学习完树转序列，序列也可以转成树，只要有中序和任一其他的序列就可以实现序列转树。

为什么一定要有中序?
前序、后序和层次序都只能确定根，无法确定子树到底是左子树还是右子树，因此必须在中序上将左右子树分开。

具体方法：
利用前序或者后序找到根节点，然后在中序中将整个序列分成左右子树。
如果给的是前序，前序序列谁和根节点靠得近，谁就是左子树的根节点，然后再在中序中找到这个根节点，利用他将左子树的点分为两部分，如此循环往复就可以还原这个二叉树。
如果给的是后序，其实本质是和前序是一样的，但是后序的根节点在最后，所以我们在找左子树的根节点时是减去右子树的所有结点后离根节点最近的结点。

线索二叉树

二叉树链式是非线性结构，没法直接找前驱和后继，所以引入线索二叉树的方法构建线性树结构。
他主要的思想是使用原先的空指针指向前驱和后继来实现线性。这里会有一个问题，无法知道你的指针代表的是孩子还是前驱与后继。所以我们引入两个新的指标（Tag）来记录是孩子还是前驱后继。
具体的结点设计如下图：

其中Tag为0代表孩子，1代表前驱或后继。
代码实现：

template <class ElemType>
struct ThreadBinTreeNode {
  ElemType data;
  ThreadBinTreeNode<ElemType> *leftChild;
  ThreadBinTreeNode<ElemType> *rightChild;
  int leftTag, rightTag;
  ThreadBinTreeNode();
  ThreadBinTreeNode(const ElemType &d,
        ThreadBinTreeNode<ElemType> *lChild=NULL,
        ThreadBinTreeNode<ElemType> *rChild=NULL,
        int leftTag=0, 	int rightTag=0);
};

致此，线索二叉树的大部分问题已经解决了，但是还存在两个问题。

中序线索二叉树在找后继的时候不一定是当前节点的孩子，而是子树的最左边的点。所以在这种情况下要特殊设置一个算法来保证后继是正确的。
算法代码如下：

  template <class ElemType>ThreadBinTreeNode<ElemType>
  *InThreadBinTree<ElemType>::GetNext(ThreadBinTreeNode<ElemType> *p) const  {
  if (p->rightTag == 1)
          p=p->rightChild;
  else  {
  p=p->rightChild;
  while (p->leftTag == 0)
          p = p->leftChild;
    }
    return p;
}

线索二叉树的插入问题
由于线索二叉树添加了新的数据成员，所以结点的插入变得更加复杂。比如要给某个结点插入一个右孩子,需要考虑本身是否有右孩子和如何修改指针。

没有右孩子
结点P原来的后继结点变为结点x的后继结点，结点p为结点x的前驱结点，结点 x成为结点p的右孩子
有右孩子
结点P原来的右子树变为结点x的右子树，结点p为结点x的前驱结点，结点 x成为结点p的右孩子。
还需修改结点p原来右子树中最左下结点的左指针，使它由原来指向结点p改为指向结点x。

template <class ElemType> void InThreadBinTree<ElemType>::
InsertRightChild(ThreadBinTreeNode<ElemType> *p, const ElemType &e) {
ThreadBinTreeNode<ElemType> *x, *q;
  if (p == NULL)	  return;
  else {
    x= new ThreadBinTreeNode<ElemType>(e, p,p->rightChild,1, p->rightTag);   //生成元素值为e结点x
    if (p->rightTag == 0)	{
      q=p->rightChild;
      while (q->leftTag == 0){
          q=q->leftChild;
          q->leftChild=x;
          }
    }
  p->rightChild=x;     p->rightTag=0;
  return;
  }
}

二叉树的应用

堆

定义：设有n个数据元素的关键字为（k0、k1、…、kn-1），如果它们满足以下的关系：ki<= k2i+1且ki<= k2i+2（或ki>= k2i+1且ki>= k2i+2）（i=0、1、…、⌊(n-2)/2⌋）则称之为堆(Heap)。
堆一定是一个完全二叉树，所以使用顺序结构进行存储。
最小堆的构造。最小堆的含义是这个树都满足父亲结点大于孩子结点。
构造最小堆的向下调整算法代码实现：

i = start;
ElemType temp = heapArr[i];
while (i < CurrentSize)
{
  j = 2*i + 1;// j为i的左孩子
    if ( j < CurrentSize &&
    heapArr[j].key > heapArr[j+1].key )
        j++;  //左右孩子中选关键字较小者
    if (temp.key<=heapArr[j].key)
            break; //不用调整
    else { // “连续” 向下调整
        heapArr[i] = heapArr[j];
        i = j;  j = 2*j+1;
  }
  heapArr[i] = temp;
}

其中，i是最后一个结点的父亲节点，j是i的左孩子。本质就是比较孩子的值，让小的上浮，直至根节点。
3. 最小堆的插入（向上调整算法）
最小堆的插入采用尾插入，再调整的方法实现。
向上调整算法具体实现代码如下：

template<class ElemType>
void MinHeap<ElemType>::FilterUp(int End)  {
  int j=End, i;
  ElemType temp=heapArr[j];
  i=(j - 1) / 2;
  while (j > 0)
  {
    if (heapArr[i] <= temp)  break;
    else {
      heapArr[j]=heapArr[i];
      j=i;   i=(j - 1) / 2;
    }
    heapArr[j]=temp;
  }
}

堆中元素删除问题
删除一般删除的是堆顶的元素，所以将最后一个元素放到堆顶，然后再进行小堆的调整。
使用的就是向下调整的算法。

为什么使用向下调整而不是向上调整？
因为向上调整是插入元素才会向上，而此处删除了一个元素，并且是从根结点开始操作，自然是使用向下调整。

哈夫曼树

哈夫曼树基本概念

树的路径：在一棵（二叉）树中由根结点到某个结点所经过的分支序列叫做由根结点到这个结点的路径。
根到结点的路径长度：由根结点到某个结点所经过的分支数称为由根结点到该结点的路径长度。
树的路径长度(Path Length，PL)：由根结点到所有叶结点的路径长度之和称为该（二叉）树的路径长度。
树的带权(Weighted)路径长度 WPL：如果(二叉)树中每一个叶结点都带有某一确定值，则称该值为结点的权值。
设一棵具有n个带权值叶结点的二叉树，那么从根结点到各个叶结点的路径长度与对应叶结点权值的乘积之和叫做二叉树的带权路径长度，记作：
$WPL=\sum_{k=1}^nW_k*L_k$

哈夫曼树定义与构造

1.定义：假设有n个权值{w1,w2,w3,…,wn},试构造一棵有n个叶子结点的二叉树,每个叶子结点带权为wi,则其中带权路径长度WPL最小的二叉树称作最优二叉树或哈夫曼树。
特点:根据哈夫曼树的定义，要使一棵二叉树的其WPL值最小，显然必须使权值越大的叶结点越靠近根结点，而权值越小的结点越远离根结点。
2.构造
哈夫曼树的构造不唯一,只是3带权路径最小,其形态也不是唯一的
具体构造方法：

由给定的n个权值{W1、W2、…、Wn}构造n棵只有一个根结点（亦为叶结点）的二叉树，从而得到一个森林F={ T1、T2、…、Tn}；
Ex: W = {7, 2, 5,4 };
在 F 中选取两棵根结点的权值最小的二叉树Ti、Tj，以Ti和Tj作为左、右子树构造一棵新的二叉树Tk。置新的二叉树Tk的根结点的权值为其左、右子树（Ti、Tj）上根结点的权值之和；
在F中删去二叉树Ti、Tj；并把新的二叉树Tk加入 F；
重复（2）和（3）步骤,直到 F 中仅剩下一棵树为止。
一句话总结就是：将带权路径值从小到大构建二叉树，权重小的放左边，大的放右边。