树和森林
树和森林
本文主要复习树和森林的内容,树和森林的所有操作都和二叉树有关,所以树和森林也会涉及到存储结构、树和森林与二叉树的转换、树和森林的变量。森林其实就是由好几棵树组成的,所以我们先讨论树。
树的存储结构
树主要有四种存储结构,分别为:双亲表示法、孩子表示法、双亲孩子表示法、孩子兄弟表示法。其中最重要的是 孩子兄弟表示法,虽然这种表示法不太符合正常逻辑,但是解决了许多操作上的问题。
双亲表示法
双亲表示法使用一个数组来存放树的结点,结点内包含两个域,分别是数据域和双亲域,双亲域存放自己的双亲结点索引,根结点双亲域为-1。
双亲表示法对于自己父亲结点的搜索较快,存储空间也比较节约,但是如果要找自己的孩子就必须遍历整个数组,比较耗时。同时找兄弟的操作也比较困难。
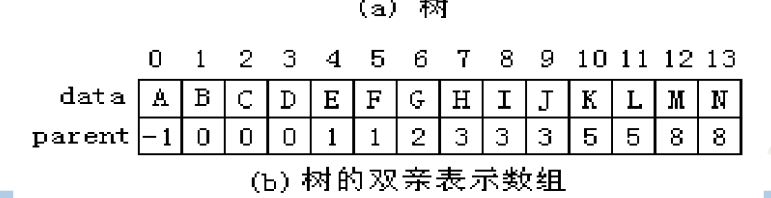
对于双亲表示法的改进就是对于结点增加两个数据域,一个是第一个孩子的索引,第二个是右兄弟的索引。
孩子表示法
孩子表示法有两种方式,一个是多重链表,另一个是孩子链表。多重链表法类似于双亲表示法的改进,不大采用这种方法。孩子链表法其实是将一个一位数组顺序存储结点信息,然后在每个数组后面连一个孩子链表,具体形式如下:
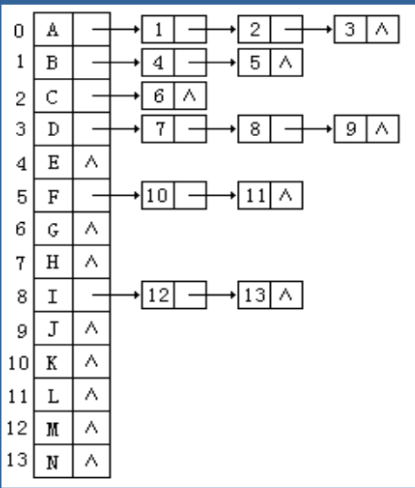
双亲孩子表示法
孩子双亲表示法就是把孩子表示法和双亲表示法结合起来,既方便孩子和兄弟的查找也方便双亲结点的查找,具体形式如下:
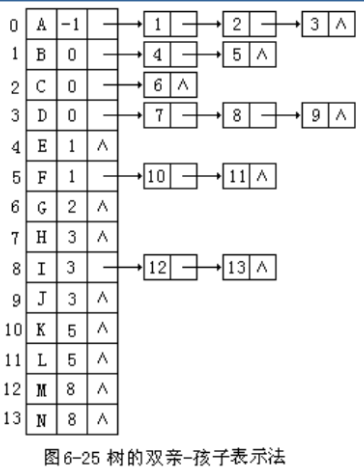
孩子兄弟表示法
孩子兄弟表示法虽然不太符合实际的逻辑,但是 该方法将树森林和已经学习过的二叉树相联系 。这种方法背后的思想是化繁为简,由为止到已知,所以孩子兄弟法需要着重掌握。
孩子兄弟表示只有两个额外的信息域,一个是第一个孩子结点指针,另一个是右兄弟的指针。仅仅通过如此简单的方法就可以将一棵树用链式的方法转化成一棵二叉树。具体形式如下:
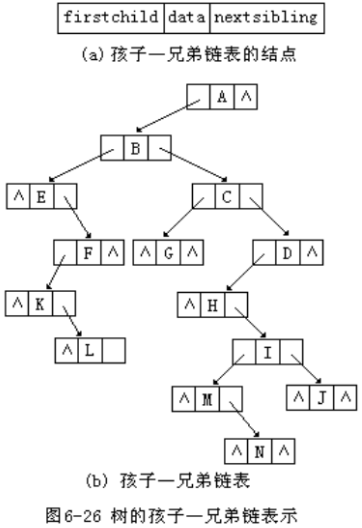
注意点:
这里的孩子兄弟法不能实现较好的双亲结点的查找,如果有需要可以增加一个信息域来存放双亲结点。
这里主要强调该方法对于树、森林转化为二叉树的作用。
树、森林转二叉树
树、森林转二叉树
树和森林转二叉树很简单,一共三步:连线、删线、美化
连线是将所有相邻结点之间加一条线。
删线就是对每一条结点只保留和第一个孩子之间的结点,删去其他的孩子结点之间连线。
对于一棵树来说,最终形成的二叉树的根节点只可能含有左子树,不可能含有右子树。而空缺的右子树是在森林情况下加入进去的。
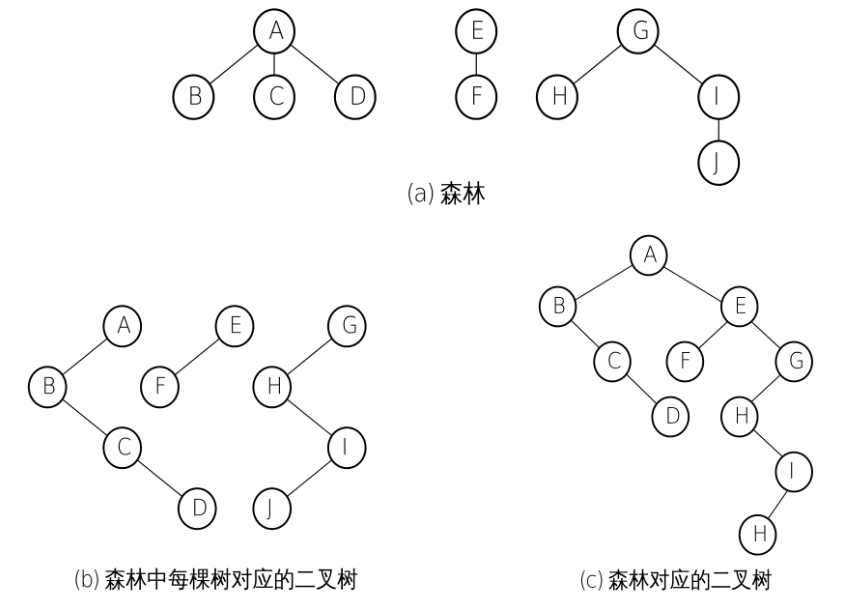
二叉树还原树和森林
二叉树还原树和森林也很简单,就是将原来删掉的线补上,添加的线删掉。对于森林来说要注意好树的数量。










